In the previous analysis of the new version of the Snowflake algorithm, we mentioned two changes made in the new version:
- The timestamp no longer constantly follows the system clock.
- The exchange of positions between node ID and timestamp. From the original:
to:
A careful student raised a question: In the new version, the algorithm is indeed monotonically increasing within a single node, but in a multi-instance deployment, it is no longer globally monotonically increasing! Because it is obvious that the node ID is in the high bits, so the generated ID with a larger node ID will definitely be greater than the ID with a smaller node ID, regardless of the chronological order. In contrast, the original algorithm, with the timestamp in the high bits and always following the system clock, can ensure that IDs generated earlier are smaller than those generated later. Only when two nodes happen to generate IDs at the same timestamp, the order of the two IDs is determined by the node ID. So, does it mean that the new version of the algorithm is wrong?
This is a great question! The fact that students can raise this question indicates a deep understanding of the essential differences between the standard Snowflake algorithm and the new version. This is commendable! Here, let's first state the conclusion: indeed, the new version of the algorithm does not possess global monotonicity, but this does not affect our original intention (to reduce database page splits). This conclusion may seem counterintuitive but can be proven.
Before providing the proof, let's briefly review some knowledge about page splits in databases. Taking the classic MySQL InnoDB as an example, InnoDB uses a B+ tree index where the leaf nodes of the primary key index also store the complete records of data rows. The leaf nodes are linked together in the form of a doubly linked list. The physical storage form of the leaf nodes is a data page, and each data page can store up to N rows of records (where N is inversely proportional to the size of each row). As shown in the diagram:
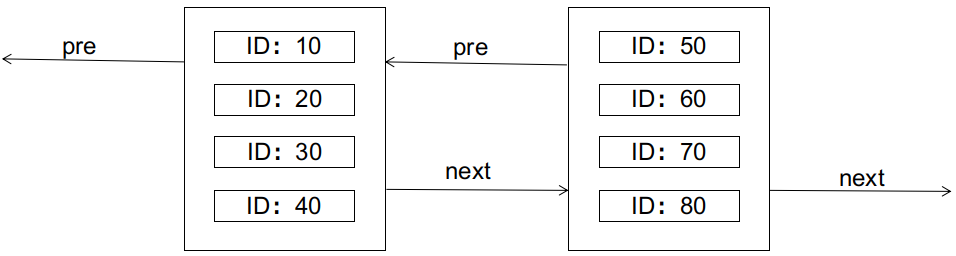The characteristics of the B+ tree require that the left node should be smaller than the right node. What happens if we want to insert a record with an ID of 25 at this point (assuming each data page can only hold 4 records)? The answer is that it will cause a page split, as shown in the diagram:
Page splits are unfriendly to I/O, requiring the creation of new data pages, copying and transferring part of the records from the old data page, etc., and should be avoided as much as possible.
Ideally, the primary key ID should be sequentially increasing (for example, setting the primary key as auto_increment). This way, a new page will only be needed when the current data page is full, and the doubly linked list will always grow sequentially at the tail, avoiding any mid-node splits.
In the worst-case scenario, if the primary key ID is randomly generated and unordered (for example, a UUID string in Java), new records will be randomly assigned to any data page. If the page is already full, it will trigger a page split.
If the primary key ID is generated by the standard Snowflake algorithm, in the best-case scenario, only one node is generating IDs within each timestamp. In this case, the algorithm's effect is equivalent to the ideal situation of sequential incrementation, similar to auto_increment. In the worst-case scenario, all nodes within each timestamp are generating IDs, and the algorithm's effect is close to unordered (but still much better than completely unordered UUIDs, as the workerId with only 10 bits limits the nodes to a maximum of 1024). In actual production, the algorithm's effectiveness depends on business traffic, and the lower the concurrency, the closer the algorithm is to the ideal scenario.
So, how does it fare with the new version of the algorithm?
The new version of the algorithm, from a global perspective, produces IDs in an unordered manner. However, for each workerId, the generated IDs are strictly monotonically increasing. Additionally, since workerId is finite, it can divide into a maximum of 1024 subsequences, each of which is monotonically increasing.
For a database, initially, the received IDs may be unordered, coming from various subsequences, as illustrated here:
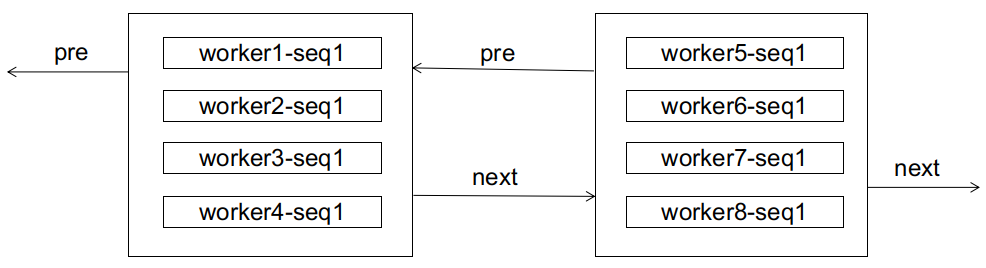
If, at this point, a worker1-seq2 arrives, it will clearly cause a page split:
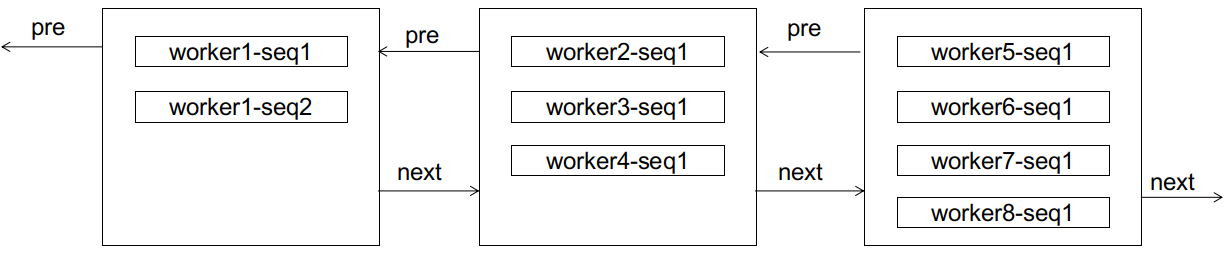
However, after the split, interesting things happen. For worker1, subsequent seq3, seq4 will not cause page splits anymore (because there is still space), and seq5 only needs to link to a new page for sequential growth (the difference is that this new page is not at the tail of the doubly linked list). Note that the subsequent IDs of worker1 will not be placed after any nodes from worker2 or beyond (thus avoiding page splits for later nodes) because they are always smaller than the IDs of worker2; nor will they be placed before the current node of worker1 (thus avoiding page splits for previous nodes) because the subsequences of worker1 are always monotonically increasing. Here, we refer to such subsequences as reaching a steady state, meaning that the subsequence has "stabilized," and its subsequent growth will only occur at the end of the subsequence without causing page splits for other nodes.
The same principle can be extended to all subsequences. Regardless of how chaotic the IDs received by the database are initially, after a finite number of page splits, the doubly linked list can always reach a stable state:
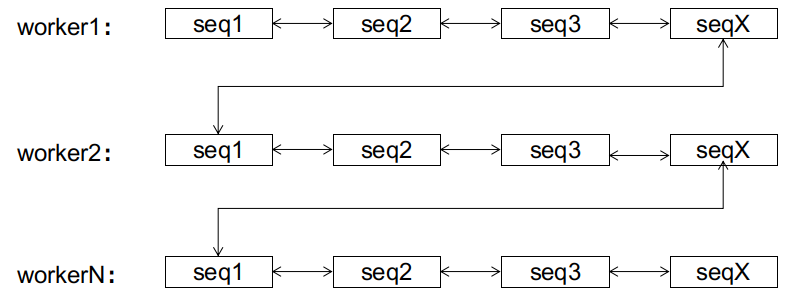
After reaching the steady state, subsequent IDs will only grow sequentially within their respective subsequences, without causing page splits. The difference between this sequential growth and the sequential growth of auto_increment is that the former has 1024 growth points (the ends of various subsequences), while the latter only has one at the end.
At this point, we can answer the question posed at the beginning: indeed, the new algorithm is not globally monotonically increasing, but the algorithm converges. After reaching a steady state, the new algorithm can achieve the same effect as global sequential incrementation.
Further Considerations
The discussion so far has focused on the continuous growth of sequences. However, in practical production, there is not only the insertion of new data but also the deletion of old data. Data deletion may lead to page merging (InnoDB, if it finds that the space utilization of two adjacent data pages is both less than 50%, it will merge them). How does this affect the new algorithm?
As we have seen in the above process, the essence of the new algorithm is to utilize early page splits to gradually separate different subsequences, allowing the algorithm to continuously converge to a steady state. Page merging, on the other hand, may reverse this process by merging different subsequences back into the same data page, hindering the convergence of the algorithm. Especially in the early stages of convergence, frequent page merging may even prevent the algorithm from converging forever (I just separated them, and now I'm merging them back together, back to square one~)! However, after convergence, only page merging at the end nodes of each subsequence has the potential to disrupt the steady state (merging the end node of one subsequence with the head node of the next subsequence). Merging on the remaining nodes of the subsequence does not affect the steady state because the subsequence remains ordered, albeit with a shorter length.
Taking Seata's server as an example, the data in the three tables of the server has a relatively short lifecycle. After a global transaction ends, the data is cleared. This is not friendly to the new algorithm, as it does not provide enough time for convergence. However, there is already a pull request (PR) for delayed deletion in the review process, and with this PR, the effect will be much better. For example, periodic weekly cleanup allows sufficient time for the algorithm to converge in the early stages, and for most of the time, the database can benefit from it. At the time of cleanup, the worst-case result is that the table is cleared, and the algorithm starts from scratch.
If you wish to apply the new algorithm to a business system, make sure to ensure that the algorithm has time to converge. For example, for user tables or similar, where data is intended to be stored for a long time, the algorithm can naturally converge. Alternatively, implement a mechanism for delayed deletion, providing enough time for the algorithm to converge.
If you have better opinions and suggestions, feel free to contact the Seata community!